How to Perform a Mergesort in Objective-C

Submitted by matt_eaton on Thu, 11/15/2018 - 11:07 AM

Tags

Objective-C

Like the quicksort or the insertion sort algorithm, the mergesort algorithm is a fundamental sorting algorithm in computer science. A while back I was looking through my old Objective-C archives and found a mergesort implementation that was created but never had seen the light of day in any project. To get some use out of this code and to share this implementation with anyone looking for a mergesort algorithm I thought I would write a brief tutorial on how my implementation of mergesort works in Objective-C. First, before getting started, there are a few things to keep in mind about this tutorial; the first is that this tutorial was created as a macOS command line application in Mojave, but any recent version of Xcode or macOS should work with this sample code. The next is this tutorial does not require extensive knowledge of Objective-C either, just fundamental Computer Science knowledge. Let's jump in!

Mergesort in Objective-C 🚀

First, before I dive into the code, let me provide a brief explanation of the mergesort algorithm. The mergesort algorithm is a sorting algorithm developed by John von Neumann back in 1945. The general idea is to take a list of data and recursively divide it into smaller lists until it is very easy to sort the elements in each list. Then, take each list and merge them back one master list. Hence the name, mergesort.

In the example I put together in Objective-C, the first thing that is done is a middle element is selected. Next, two smaller array are created. One array from 0 up to the middle element, the other array from the middl element to the end of the array.

int count = (int)[unsortedArray count];
if (count < 2) {
    return unsortedArray;
}
int middle = count / 2;
NSArray *leftArray = [unsortedArray subarrayWithRange: NSMakeRange(0, middle)];
NSArray *rightArray = [unsortedArray subarrayWithRange: NSMakeRange(middle, (count - middle))];

Next, those smaller arrays are sent into a recursive method called mergeArray: and each element is evaluated and stacked up in at the start of a NSMutableArray called returnArray. Then each of the remaining elements in leftArray and rightArray are added to the end of the returnArray and the returnArray is sent back to be run through the recursive process again.

- (NSArray *) mergeArray:(NSArray *)leftArray rightArray:(NSArray *)rightArray {
 
    NSMutableArray *returnArray = [NSMutableArray array];
    int i = 0, e = 0;
 
    while (i < [leftArray count] && e < [rightArray count]) {
        int leftValue = [[leftArray objectAtIndex:i] intValue];
        int rightValue = [[rightArray objectAtIndex:e] intValue];
        if (leftValue < rightValue) {
            [returnArray addObject: [leftArray objectAtIndex:i++]];
        } else {
            [returnArray addObject: [rightArray objectAtIndex:e++]];
        }
    }
 
    while (i < [leftArray count]) {
        [returnArray addObject: [leftArray objectAtIndex:i++]];
    }
 
    while (e < [rightArray count]) {
        [returnArray addObject: [rightArray objectAtIndex:e++]];
    }
 
    return returnArray;
}

This line of code below is what drives the recursion of splitting the larger arrays into smaller ones. The entire process keeps running until there are less than 2 elements in each array.

NSArray *returnArray = [self mergeArray: [self mergeSortArray: leftArray] rightArray: [self mergeSortArray: rightArray]];

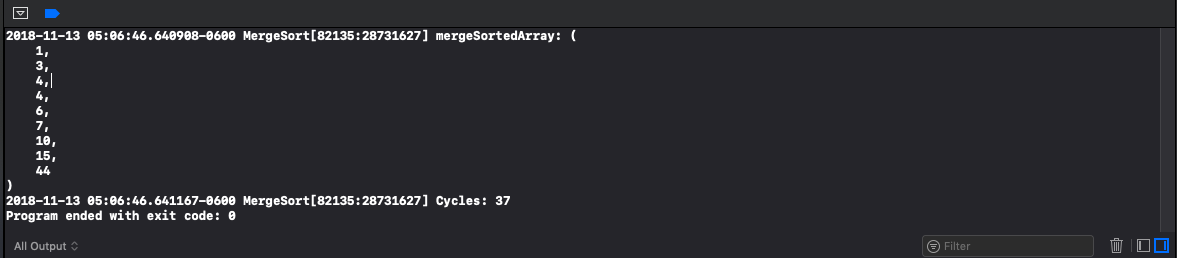
Once each array is returned the final returnArray is available by reference and is returned from the mergeSortArray: method. See an example of the entire algorithm below. The time complexity of the mergesort algorithm in the worst case is O(n * log(n)). The space complexity of the mergesort algorithm is O(3 * n) or just O(n) for each array used.

//
//  main.m
//  MergeSort
//
//  Created by Matt Eaton on 11/13/18.
//  Copyright © 2018 Matt Eaton. All rights reserved.
//
 
#import <Foundation/Foundation.h>
 
@interface MergeSort: NSObject
 
- (NSArray *) mergeSortArray:(NSArray *)unsortedArray;
@end
 
@implementation MergeSort
 
- (NSArray *) mergeArray:(NSArray *)leftArray rightArray:(NSArray *)rightArray {
 
    NSMutableArray *returnArray = [NSMutableArray array];
    int i = 0, e = 0;
 
    while (i < [leftArray count] && e < [rightArray count]) {
        int leftValue = [[leftArray objectAtIndex:i] intValue];
        int rightValue = [[rightArray objectAtIndex:e] intValue];
        if (leftValue < rightValue) {
            [returnArray addObject: [leftArray objectAtIndex:i++]];
        } else {
            [returnArray addObject: [rightArray objectAtIndex:e++]];
        }
    }
 
    while (i < [leftArray count]) {
        [returnArray addObject: [leftArray objectAtIndex:i++]];
    }
 
    while (e < [rightArray count]) {
        [returnArray addObject: [rightArray objectAtIndex:e++]];
    }
 
    return returnArray;
}
 
 
- (NSArray *) mergeSortArray:(NSArray *)unsortedArray {
 
    // Time complexity: Worst case is: O(n * log(n)).
    // Space complexity: O(3 * n) or O(n) due to the 3 NSArrays that are used.
 
 
    int count = (int)[unsortedArray count];
    if (count < 2) {
        return unsortedArray;
    }
    int middle = count / 2;
    NSArray *leftArray = [unsortedArray subarrayWithRange: NSMakeRange(0, middle)];
    NSArray *rightArray = [unsortedArray subarrayWithRange: NSMakeRange(middle, (count - middle))];
 
    NSArray *returnArray = [self mergeArray: [self mergeSortArray: leftArray] rightArray: [self mergeSortArray: rightArray]];
    return returnArray;
}
 
@end
 
int main(int argc, const char * argv[]) {
    @autoreleasepool {
        NSArray *mergeSorttData = @[@4, @3, @10, @44, @6, @4, @1, @7, @15];
 
        MergeSort *ms = [[MergeSort alloc] init];
        ms.cycles = 0;
        NSArray *mergeSortedArray = [ms mergeSortArray: mergeSorttData];
        NSLog(@"mergeSortedArray: %@", mergeSortedArray);
    }
    return 0;
}

In Summary ⌛️

In summary I hope that this tutorial provides more information on the ever popular mergesort algorithm and how to implement it in Objective-C. This example is a bit different than some standard library implementations out there because of the Objective-C APIs, but the base concepts are still present. I hope you enjoyed this tutorial and if you have any questions, comments, or concerns, please leave a comment below and I will make sure to address it as soon as I am able to. Thank you very much for reading and the code from this tutorial can be downloaded from my Github here.

Credits: Cover image designed by Freepik.

Member for

3 years 9 months

Matt Eaton

Long time mobile team lead with a love for network engineering, security, IoT, oss, writing, wireless, and mobile. Avid runner and determined health nut living in the greater Chicagoland area.

Twitter

Github